1.求链表倒数第K个节点(单向链表)?
思路:采用双指针法。P1指向表头,P2指向P1相隔K的节点,同时向后移动,当P2到达表尾(P2->next=null), P1即倒数第K个节点。
2.判断链表是否有环?
首先循环链表是带环链表的一种特殊情况。
思想:类似于生活中跑步追赶的问题。两个人从相同起点出发,其中一个人的速度比另外一个人快,结果经过一段时间后,速度快的人会追上速度慢的人,此时速度快的人比慢的人多跑了一圈,这样就证明存在了环。
方法:两个指针P1和P2,从链表的起点开始,P1一次移动一个步长,P2一次移动2个步长,若两个指针相等(并且不等于null),则P2绕了n圈之后追上了P1,则链表存在环。
3.判断两个链表是否存在交点?
思想:若L1、L2都无环,直接遍历L1和L2,找到他们的尾节点,若尾节点相同,则必定相交。时间复杂度O(m+n),空间复杂度O(1)。若一个链表有环,一个链表无环,则必不可能相交。若两个都有环,遍历L1环上的每一个节点是否和L2环上的某个节点相等。
4.一个链表成环,环的入口在哪里?
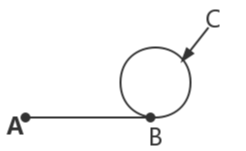
设A为起点,B为入口,C为第一次相遇点。且AB=a,BC=x,链表长度为L,环的一圈长度为r。假设相遇时,fast节点走了2s,slow节点走了s。则有
$$
s+nr=2s\\则有 \ s=nr\\而a+x=s,r=L-a\\则有a+x=(n-1)r+r=(n-1)r+L-a\\则a=(n-1)r+L-a-x。
$$
而L-a-x为CB的长度(不是BC),则有从链表头A到环入口B等于(n-1)次循环内环加上相遇点到环入口的距离CB,则可让slow节点从A出发,fast节点从C出发。当两者再次相遇的时候就是入口B。(这里可能比较绕,建议大家自己在草稿纸上画一下,就很明显了)
5.如何求单链表中环的长度?
思路:仍然采用双指针,一个指针速度为2,一个指针速度为1,则第一次相遇的时候存在:
$$
2t_1-t_1=kr
$$
第二次相遇的时候有:
$$
2t_2-t_2=(k+1)r
$$
两式相减有:
$$
t_2-t_1=r
$$
因此只需要记录第一次相遇时前进的步数t1和第二次相遇前进的步数t2,即可求出环的长度。